小菜鸟

java菜鸟号正在起航

0%

图简介

发表于 更新于 分类于 阅读次数： 32 Valine：
本文字数： 3.8k 阅读时长 ≈ 3 分钟

图（Graph）：复杂关系的数学模型与遍历算法

图是一种用于描述多对多关系的数据结构，由节点（顶点） 和边组成，广泛应用于地图导航、社交网络、电路设计等场景。与树的 “层次化” 结构不同，图的节点可以任意连接，能更灵活地表达现实世界中的复杂关系。

图的基本概念与分类

核心定义

  • 顶点（Vertex）：图中的基本元素（如城市、用户）。
  • 边（Edge）：连接两个顶点的关系（如道路、好友关系）。
  • 邻接：若两个顶点之间有边相连，则互为邻接点。

图的分类

（1）按边的方向性
  • 无向图：边没有方向，顶点u与v的边可表示为(u, v)，且(u, v) = (v, u)（如双向道路）。
  • 有向图：边有方向，顶点u到v的边表示为<u, v>，与<v, u>不同（如单向街道、微博关注）。
（2）按边的完整性
  • 完全图：
    • 无向完全图：每个顶点与其他所有顶点都有边，含n个顶点的无向完全图有n(n-1)/2条边。
    • 有向完全图：每对顶点之间有两条方向相反的边，含n个顶点的有向完全图有n(n-1)条边。
（3）其他常见类型
  • 稀疏图：边数远少于完全图的图（如社交网络中用户的好友关系）。
  • 稠密图：边数接近完全图的图（如电路中的节点连接）。

图的存储结构

图的存储需高效表达顶点与边的关系，常用方式有邻接矩阵和邻接表。

1. 邻接矩阵（Adjacency Matrix）

用n×n的二维数组matrix表示图（n为顶点数），其中：

  • matrix[i][j] = 1（或权值）：顶点i与j之间有边。
  • matrix[i][j] = 0：顶点i与j之间无边。
（1）无向图的邻接矩阵

  • 矩阵对称（matrix[i][j] = matrix[j][i]）。
  • 主对角线为 0（顶点自身无环）。
  • 顶点i的度（边数）= 第i行（或列）中 1 的个数。

示例：

1
2
3
4
   0 1 2
0 [0,1,0]
1 [1,0,1]
2 [0,1,0]

表示顶点 0-1、1-2 之间有边，顶点 0 的度为 1，顶点 1 的度为 2。

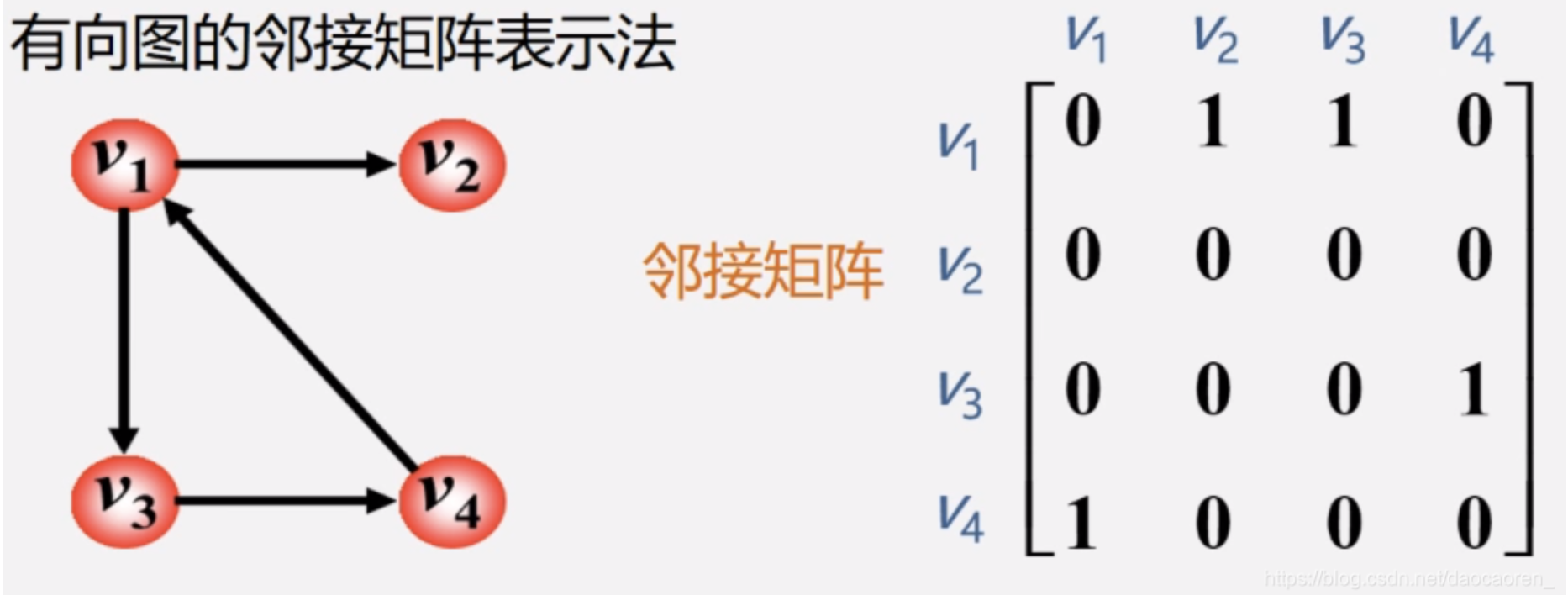
（2）有向图的邻接矩阵

  • 矩阵不对称（matrix[i][j]与matrix[j][i]可不同）。
  • 顶点i的出度= 第i行中 1 的个数（从i出发的边）。
  • 顶点i的入度= 第i列中 1 的个数（指向i的边）。

示例：

1
2
3
4
   0 1 2
0 [0,1,0]
1 [0,0,1]
2 [1,0,0]

表示边<0,1>、<1,2>、<2,0>，顶点 0 的出度为 1，入度为 1。

邻接矩阵的优缺点
  • 优点：判断两顶点是否相邻效率高（O(1)），适合稠密图。
  • 缺点：空间复杂度O(n²)，稀疏图会浪费大量空间。

2. 邻接表（Adjacency List）

由顶点数组和边链表组成：

  • 顶点数组：存储所有顶点。
  • 边链表：每个顶点对应一个链表，存储其邻接顶点。
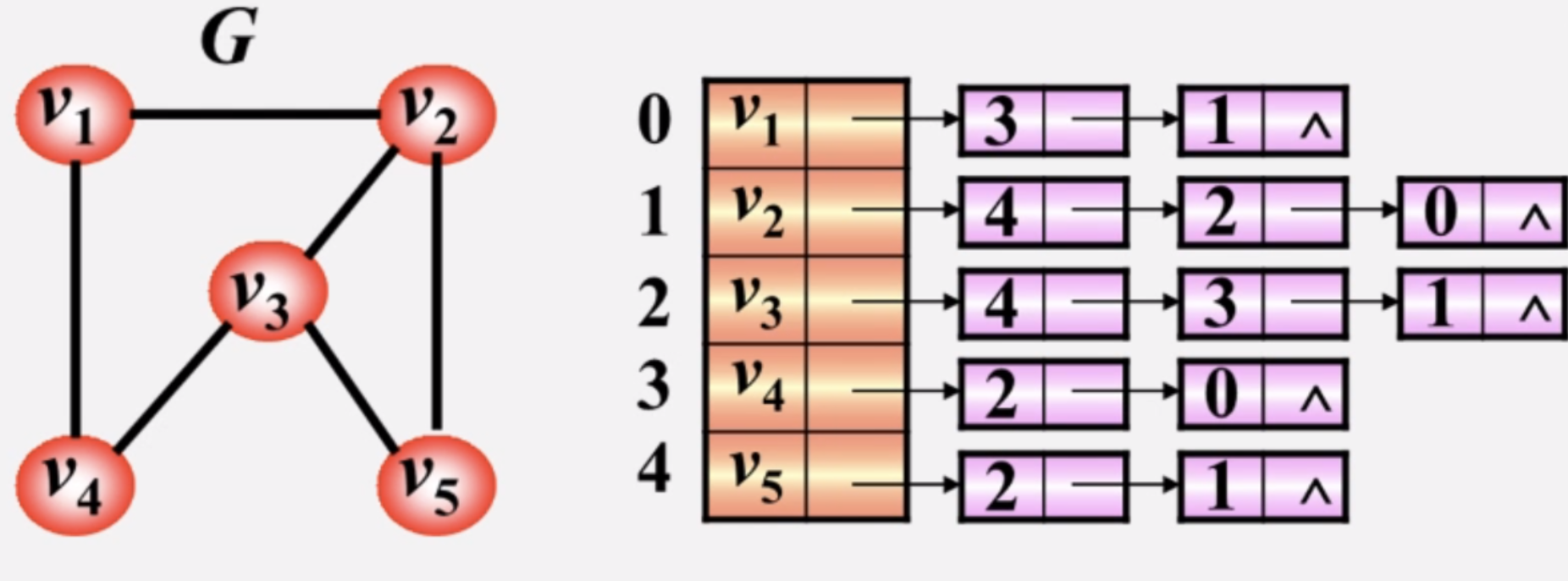
（1）无向图的邻接表

  • 每个边会在两个顶点的链表中出现（如(u, v)同时在u和v的链表中）。
  • 顶点i的度 = 对应链表的长度。

示例：

1
2
3
顶点0：[1]
顶点1：[0, 2]
顶点2：[1]

表示边 (0,1)、(1,2)。

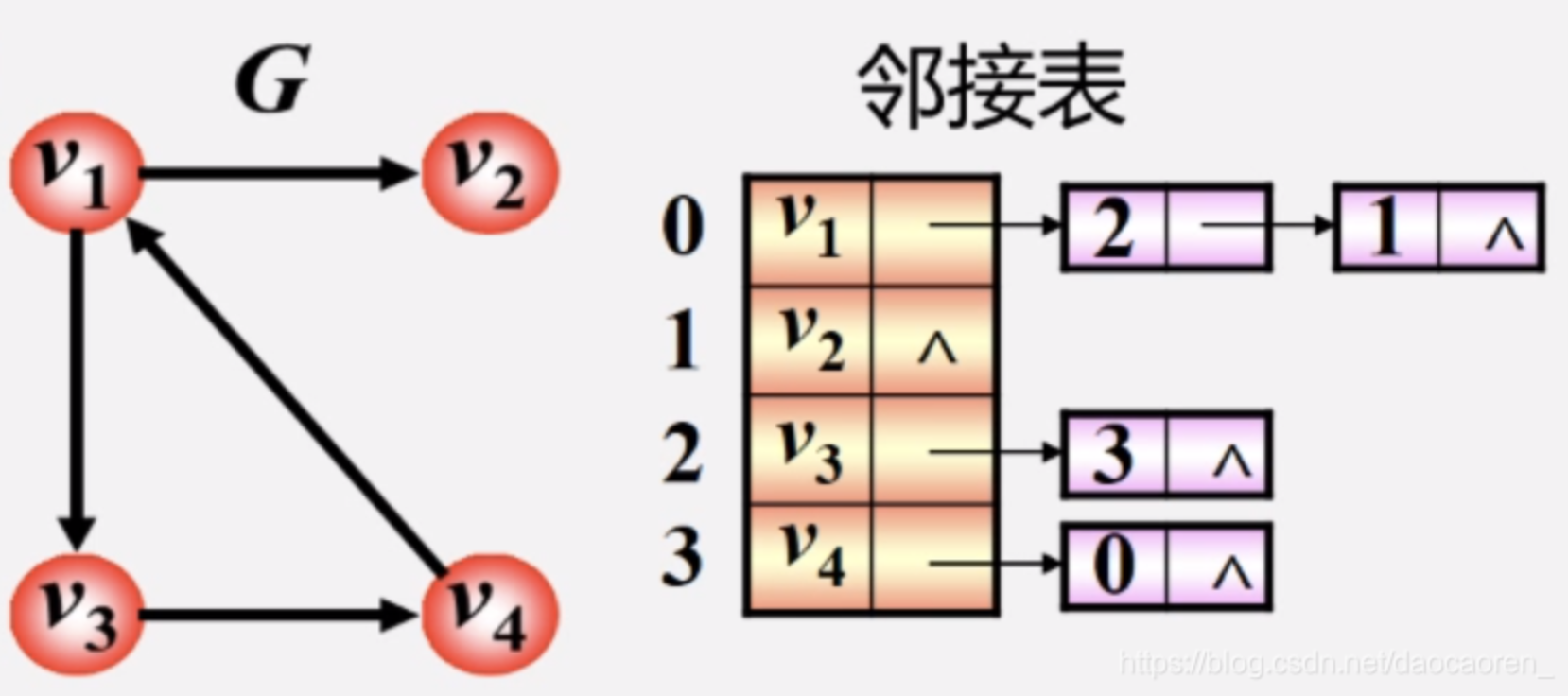
（2）有向图的邻接表

  • 每个边仅在起点的链表中出现（如<u, v>仅在u的链表中）。
  • 顶点i的出度 = 对应链表的长度；入度需遍历所有链表统计。

示例：

1
2
3
顶点0：[1]
顶点1：[2]
顶点2：[0]

表示边<0,1>、<1,2>、<2,0>。

邻接表的优缺点
  • 优点：空间复杂度O(n + e)（e为边数），适合稀疏图。
  • 缺点：判断两顶点是否相邻需遍历链表（O(k)，k为链表长度）。

图的遍历算法

遍历是按一定规则访问图中所有顶点的过程，核心算法有深度优先搜索（DFS） 和广度优先搜索（BFS）。

1. 深度优先搜索（DFS）

思想：从起点出发，沿一条路径深入到底，无法前进时回溯，探索其他路径（类似迷宫探索）。

步骤：
  1. 访问起点，标记为已访问。
  2. 递归访问起点的未访问邻接点，重复步骤 1。
  3. 若所有邻接点均已访问，回溯至前一顶点，继续探索其他路径。
代码实现（邻接表）：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public class GraphDFS {
    private List<List<Integer>> adjList; // 邻接表
    private boolean[] visited;          // 标记顶点是否访问

    public GraphDFS(int n) {
        adjList = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            adjList.add(new ArrayList<>());
        }
        visited = new boolean[n];
    }

    // 添加边
    public void addEdge(int u, int v) {
        adjList.get(u).add(v);
        adjList.get(v).add(u); // 无向图需双向添加
    }

    // 深度优先遍历
    public void dfs(int start) {
        visited[start] = true;
        System.out.print(start + " ");

        for (int neighbor : adjList.get(start)) {
            if (!visited[neighbor]) {
                dfs(neighbor); // 递归访问未访问的邻接点
            }
        }
    }

    public static void main(String[] args) {
        GraphDFS graph = new GraphDFS(3);
        graph.addEdge(0, 1);
        graph.addEdge(1, 2);
        System.out.println("DFS遍历结果：");
        graph.dfs(0); // 输出：0 1 2
    }
}
时间复杂度：
  • 邻接矩阵：O(n²)（需遍历每行）。
  • 邻接表：O(n + e)（每个顶点和边访问一次）。

2. 广度优先搜索（BFS）

思想：从起点出发，逐层访问所有邻接点（先访问一度关系，再二度关系，类似水波扩散）。

步骤：
  1. 访问起点，标记为已访问，入队。
  2. 出队一个顶点，访问其所有未访问邻接点，标记后入队。
  3. 重复步骤 2，直至队列为空。
代码实现（邻接表）：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public class GraphBFS {
    private List<List<Integer>> adjList;
    private boolean[] visited;

    public GraphBFS(int n) {
        adjList = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            adjList.add(new ArrayList<>());
        }
        visited = new boolean[n];
    }

    public void addEdge(int u, int v) {
        adjList.get(u).add(v);
        adjList.get(v).add(u); // 无向图
    }

    // 广度优先遍历
    public void bfs(int start) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(start);
        visited[start] = true;

        while (!queue.isEmpty()) {
            int curr = queue.poll();
            System.out.print(curr + " ");

            for (int neighbor : adjList.get(curr)) {
                if (!visited[neighbor]) {
                    visited[neighbor] = true;
                    queue.add(neighbor);
                }
            }
        }
    }

    public static void main(String[] args) {
        GraphBFS graph = new GraphBFS(3);
        graph.addEdge(0, 1);
        graph.addEdge(1, 2);
        System.out.println("BFS遍历结果：");
        graph.bfs(0); // 输出：0 1 2
    }
}
应用场景：
  • 最短路径问题（如 “从 A 到 B 的最短路径”，路径长度按边数计算）。
  • 关系网搜索（如 “找到离 A 最近的目标用户”）。

图的典型应用

  • 地图导航：用图表示道路网络，Dijkstra 算法或 Floyd 算法求解最短路径。
  • 社交网络：用图表示用户关系，BFS 可查找 “两人之间的最短好友链”。
  • 电路设计：用图表示元件连接，DFS 可检测电路是否存在环路。
  • 编译器：用有向图表示语法规则，检测语法是否存在冲突。

总结

图是描述复杂关系的强大工具，其存储结构（邻接矩阵 / 邻接表）需根据图的稀疏程度选择。DFS 和 BFS 是遍历图的基础算法，分别适用于路径探索和最短路径求解

相关文章

欢迎关注我的其它发布渠道

表情 | 预览
Powered By Valine
v1.3.10