小菜鸟

java菜鸟号正在起航

0%

迪杰斯特拉算法

发表于 更新于 分类于 阅读次数： 46 Valine： 0
本文字数： 9.7k 阅读时长 ≈ 9 分钟

迪杰斯特拉算法（Dijkstra’s Algorithm）：带权图中的最短路径求解

迪杰斯特拉算法是一种用于带权有向图（边权重为非负数） 的最短路径算法，核心是从起点出发，逐步找到到所有其他节点的总权重最小的路径。与广度优先算法（仅适用于边权重相同的场景，如 “最少换乘”）不同，它能处理边权重不同的情况（如 “最短时间”“最少成本”），广泛应用于导航系统、网络路由等领域。

迪杰斯特拉算法的核心思想

基本原理

算法基于贪心策略：每次选择 “当前已知最短路径可达的节点”，通过该节点更新其邻居的最短路径，直到所有节点都被处理。

  • 核心目标：找到从起点到其他所有节点的最短路径（总权重最小）。
  • 适用条件：图中边的权重必须为非负数（若存在负权重，算法会失效，需用贝尔曼 - 福特算法）。

关键概念

  • 起点：路径的起始节点（如 “出发地 A”）。
  • 权重：边的 “代价”（如时间、距离、成本等，必须≥0）。
  • 最短路径：从起点到某节点的所有路径中，总权重最小的路径。
  • 已处理节点：已确定最短路径的节点（一旦处理，不再更新其路径）。

迪杰斯特拉算法的步骤

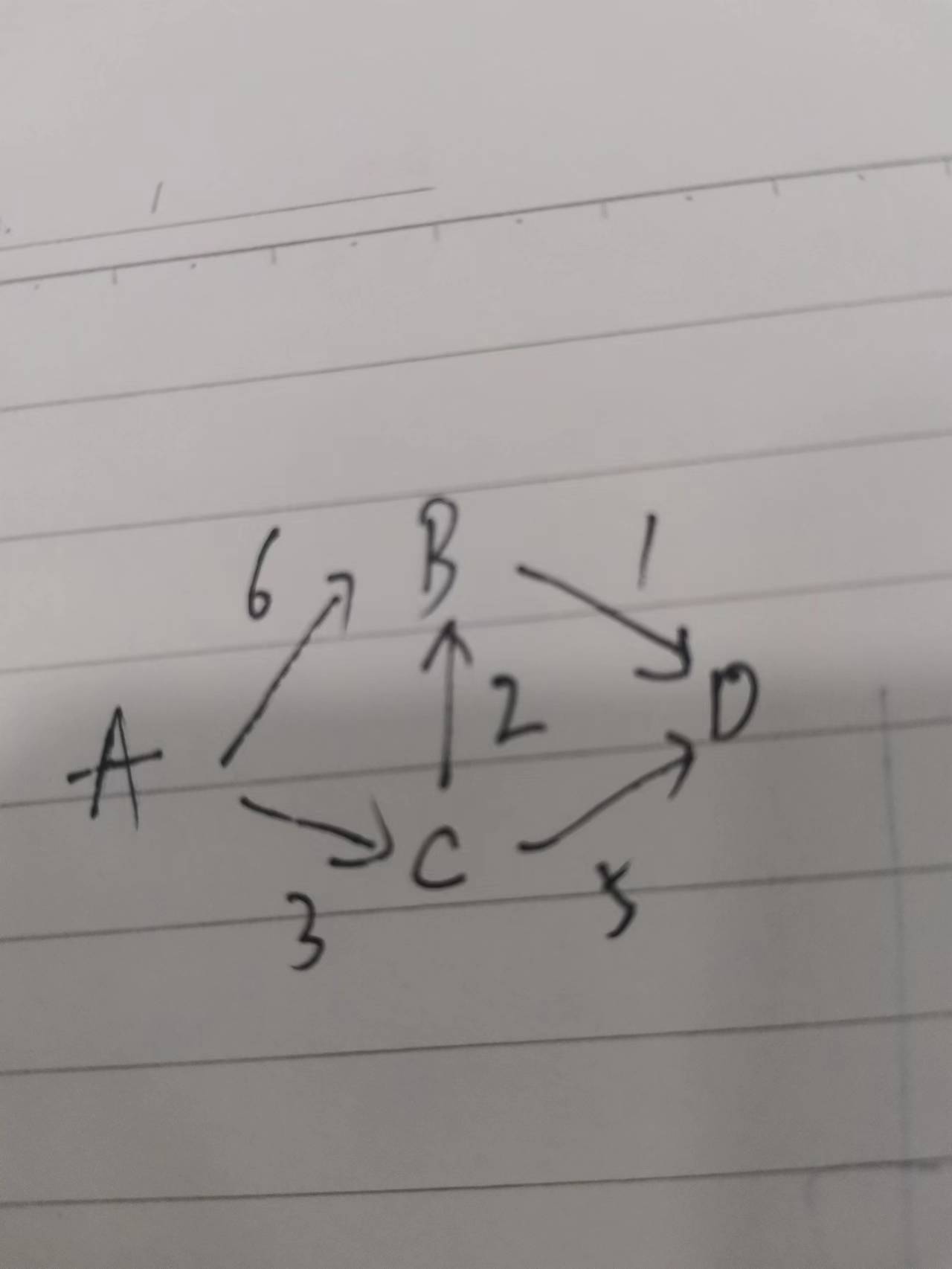
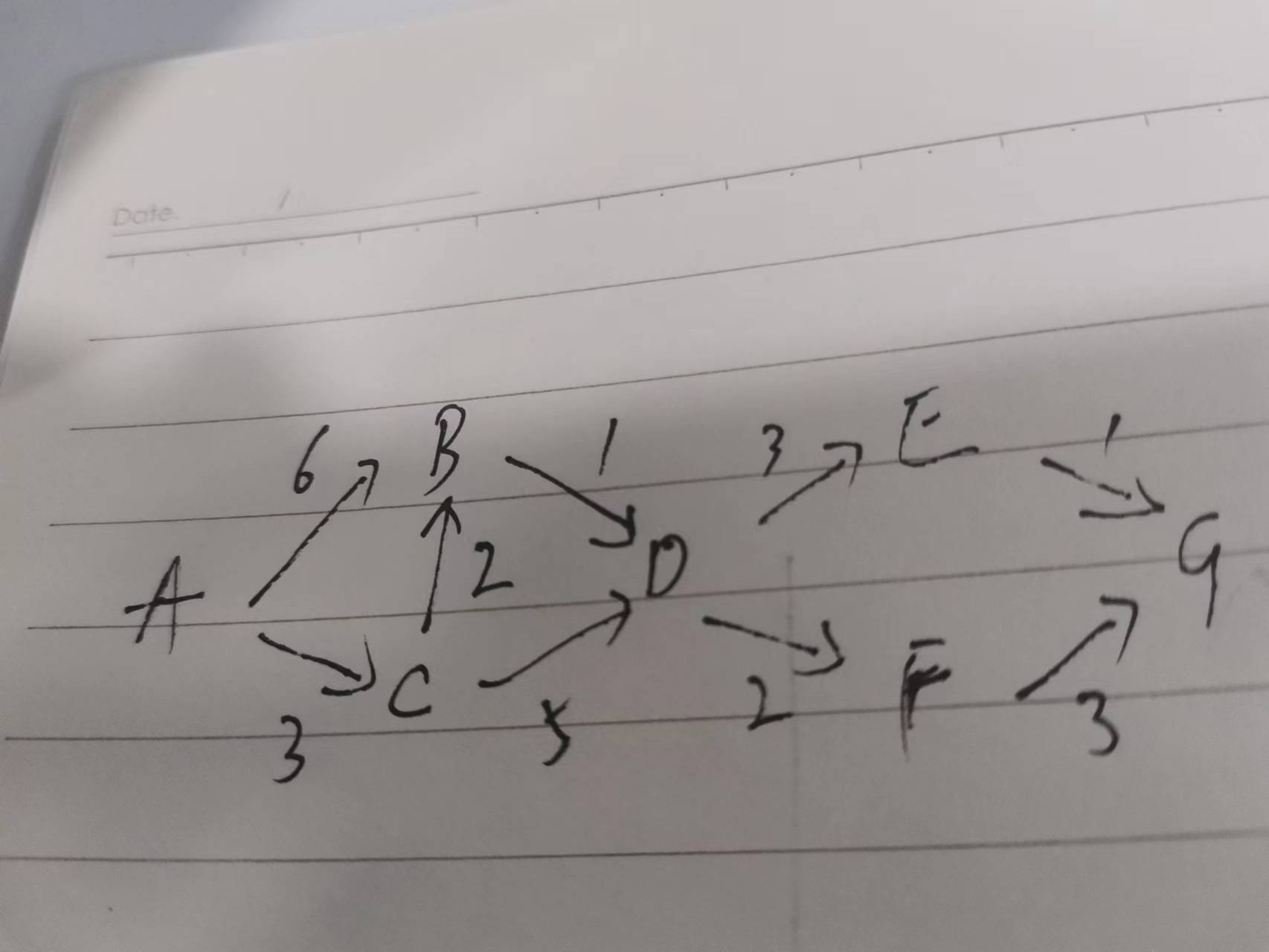
以 “从 A 到 G 的最短路径” 为例（图中边权重为时间，单位：分钟），算法步骤如下：

步骤 1：初始化数据

  • 图的表示：用邻接表存储节点间的权重（如A的邻居为B(6)、C(3)，表示 A 到 B 需 6 分钟，A 到 C 需 3 分钟）。
  • 距离表（costMap）：记录从起点到各节点的当前最短距离，初始时起点距离为 0，其他节点为 “无穷大”（表示暂不可达）。
  • 父节点表（parentMap）：记录各节点的前序节点，用于最终回溯路径。
  • 已处理集合（processed）：记录已确定最短路径的节点（初始时仅包含起点）。

步骤 2：迭代寻找最短路径

  1. 选择当前最短路径可达的节点：从 “未处理节点” 中，选出距离起点最近的节点（记为u）。
  2. 更新u的邻居的最短路径：对于u的每个邻居v，计算 “起点→u→v” 的总距离（起点到 u 的距离 + u 到 v 的权重）。若该距离小于v当前的已知最短距离，则更新v的距离和父节点（设为u）。
  3. 标记u为已处理：一旦u被处理，其最短路径不再变更（因权重非负，后续路径不可能更短）。
  4. 重复：直到所有节点都被处理，或找到目标节点的最短路径。

示例：从 A 到 G 的最短路径计算

图结构（边权重为时间）

1
2
3
4
5
A → B（6）；A → C（3）  
C → B（2）；C → D（5）  
B → D（1）  
D → E（3）；D → F（2）  
E → G（1）；F → G（3）

算法执行过程

  1. 初始化：
    • 距离表：A:0，B:∞，C:∞，D:∞，E:∞，F:∞，G:∞
    • 已处理：{A}
  2. 第一次迭代：
    • 未处理节点中，A 的邻居B(6)和C(3)，选最近的C（距离 3）。
    • 更新C的邻居：
      • B：A→C→B总距离3+2=5（小于原∞）→ 更新B:5，父节点C。
      • D：A→C→D总距离3+5=8 → 更新D:8，父节点C。
    • 已处理：{A, C}
  3. 第二次迭代：
    • 未处理节点中，最近的是B（距离 5）。
    • 更新B的邻居D：
      • A→C→B→D总距离5+1=6（小于原 8）→ 更新D:6，父节点B。
    • 已处理：{A, C, B}
  4. 第三次迭代：
    • 未处理节点中，最近的是D（距离 6）。
    • 更新D的邻居：
      • E：6+3=9 → 更新E:9，父节点D。
      • F：6+2=8 → 更新F:8，父节点D。
    • 已处理：{A, C, B, D}
  5. 第四次迭代：
    • 未处理节点中，最近的是F（距离 8）。
    • 更新F的邻居G：8+3=11 → 更新G:11，父节点F。
    • 已处理：{A, C, B, D, F}
  6. 第五次迭代：
    • 未处理节点中，最近的是E（距离 9）。
    • 更新E的邻居G：9+1=10（小于原 11）→ 更新G:10，父节点E。
    • 已处理：{A, C, B, D, F, E}
  7. 结束：所有节点处理完毕，G的最短距离为 10，路径为A→C→B→D→E→G。

代码实现与解析

核心数据结构

  • graphMap：邻接表，存储节点及其邻居的权重（Map<String, Map<String, Integer>>）。
  • costMap：记录起点到各节点的当前最短距离（Map<String, Integer>）。
  • parentMap：记录路径的父节点，用于回溯完整路径（Map<String, String>）。
  • processed：已处理节点集合（Set<String>）。

代码逻辑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
import java.util.*;

public class Dijkstra {
    // 图的邻接表：key=节点，value=该节点的邻居及权重
    static Map<String, Map<String, Integer>> graphMap = new HashMap<>();
    // 起点到各节点的最短距离
    static Map<String, Integer> costMap = new HashMap<>();
    // 已处理的节点
    static Set<String> processed = new HashSet<>();
    // 父节点表：记录路径
    static Map<String, String> parentMap = new HashMap<>();
    // 起点
    static final String START = "A";

    static {
        // 初始化图
        graphMap.put("A", new HashMap<String, Integer>() {{
            put("B", 6);
            put("C", 3);
        }});
        graphMap.put("C", new HashMap<String, Integer>() {{
            put("B", 2);
            put("D", 5);
        }});
        graphMap.put("B", new HashMap<String, Integer>() {{
            put("D", 1);
        }});
        graphMap.put("D", new HashMap<String, Integer>() {{
            put("E", 3);
            put("F", 2);
        }});
        graphMap.put("E", new HashMap<String, Integer>() {{
            put("G", 1);
        }});
        graphMap.put("F", new HashMap<String, Integer>() {{
            put("G", 3);
        }});
        graphMap.put("G", new HashMap<>()); // G无邻居

        // 初始化距离表：起点距离0，其他为无穷大
        graphMap.keySet().forEach(node -> {
            costMap.put(node, node.equals(START) ? 0 : Integer.MAX_VALUE);
        });

        // 初始化已处理集合（仅包含起点）
        processed.add(START);
    }

    public static void main(String[] args) {
        // 处理所有节点
        while (processed.size() < graphMap.size()) {
            dijkstraStep();
        }

        // 输出结果
        System.out.println("从" + START + "到G的最短距离：" + costMap.get("G")); // 10
        System.out.println("路径：" + getPath("G")); // A->C->B->D->E->G
    }

    // 单步处理：找到下一个最短节点并更新邻居
    private static void dijkstraStep() {
        String currentNode = findNextShortestNode(); // 找到未处理的最短距离节点
        if (currentNode == null) return;

        int currentCost = costMap.get(currentNode); // 起点到当前节点的距离
        // 更新当前节点的所有邻居
        for (Map.Entry<String, Integer> neighbor : graphMap.get(currentNode).entrySet()) {
            String neighborNode = neighbor.getKey();
            int newCost = currentCost + neighbor.getValue(); // 起点→currentNode→neighborNode的距离

            // 若新距离更短，则更新
            if (newCost < costMap.get(neighborNode)) {
                costMap.put(neighborNode, newCost);
                parentMap.put(neighborNode, currentNode); // 记录父节点
            }
        }

        processed.add(currentNode); // 标记为已处理
    }

    // 找到未处理的最短距离节点
    private static String findNextShortestNode() {
        int minCost = Integer.MAX_VALUE;
        String minNode = null;

        for (String node : graphMap.keySet()) {
            if (!processed.contains(node) && costMap.get(node) < minCost) {
                minCost = costMap.get(node);
                minNode = node;
            }
        }
        return minNode;
    }

    // 回溯路径（从目标节点到起点）
    private static String getPath(String target) {
        StringBuilder path = new StringBuilder(target);
        String current = target;
        while (!current.equals(START)) {
            current = parentMap.get(current);
            path.insert(0, current + "->");
        }
        return path.toString();
    }
}

算法优化与时间复杂度

时间复杂度

  • 基础实现：每次查找下一个最短节点需遍历所有未处理节点（O(V)），共需O(V)次迭代，总时间复杂度为O(V²)（V为节点数）。
  • 优化实现：用优先队列（最小堆） 存储未处理节点，查找最短节点的时间从O(V)降至O(logV)，总时间复杂度优化为O((V + E)logV)（E为边数），适合边数较少的稀疏图。

局限性

  • 仅适用于非负权重的图（若存在负权重，已处理节点的最短路径可能被后续更短路径推翻）。
  • 无法处理有环图中的负权重环（会导致路径无限缩短）。

应用场景

  • 导航系统：计算两地之间的最短时间 / 距离路径（如高德地图、Google Maps）。
  • 网络路由：路由器之间计算数据传输的最短路径（如 OSPF 协议）。
  • 资源分配：在带成本的任务依赖图中，找到从起点到目标的最低成本路径。

总结

迪杰斯特拉算法通过贪心策略，逐步确定从起点到各节点的最短路径，核心是 “每次处理当前最短可达节点并更新其邻居”。它能高效处理非负权重的带权图，是解决最短路径问题的经典算法

迪杰斯特拉算法

之前在进行最短路径计算时使用了广度优先算法，但是找出的只是换乘最少的路径，每次所用的时间其实是不一样的，如果要找出用时最短的路径，可以使用迪杰斯特拉算法(Dijkstra)

如上述路线，从A到D，如果使用广度优先算法的话会得到A->B->D，花费7分钟。而其实最短时间是A->C->B->D，花费6分钟。

迪杰斯特拉算法包含四个步骤

  • 找出可在最短时间内到达的节点，站在A点，不知道该前往B点还是C点时，此时由于还不知道前往终点需要多长时间，假设是无穷大。此时C点是最近的

  • 第一步算出来C点是距离起点最近的，这一步需要计算出经过C点到其他各邻居节点所需的时间

    A->C->B 需要5分钟

    A->C->D需要8分钟

    OK。此时找到了一条前往B的更短路径。直接前往B需要6分钟，经C之后前往B只需要5分钟。

    所以更新一下到各节点的时间开销

    • 前往B点的路径时间从6分钟缩短到了5分钟
    • 前往终点的时间从无穷大缩短到了8分钟

  • 重复前两步操作。重复第一步时排除掉第一次选出的C点，所以选出的点是B点。重复第二步更新B点所有邻居节点的开销。

    此时发现达到终点的时间变为了6分钟。

  • 最终算出到达终点的最短时间

使用的是贪心算法

在迪杰斯特拉算法中，给每段都分配了一个权重，找到的是总权重最小的路径

举个栗子

计算A到G的总权重最小路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
public class Dijkstra {

    // 到达所有邻居节点的
    static Map<String, Map<String,Integer>> graphMap = new HashMap<>();
    static {
        Map<String,Integer> aNeighborMap = new HashMap<>();
        graphMap.put("A",aNeighborMap);
        aNeighborMap.put("B",6);
        aNeighborMap.put("C",3);

        // C到达所有邻居节点的
        Map<String,Integer> cNeighborMap = new HashMap<>();
        graphMap.put("C",cNeighborMap);
        cNeighborMap.put("B",2);
        cNeighborMap.put("D",5);

        // B到达所有邻居节点的
        Map<String,Integer> bNeighborMap = new HashMap<>();
        graphMap.put("B",bNeighborMap);
        bNeighborMap.put("D",1);

        // D到达所有邻居节点的
        Map<String,Integer> dNeighborMap = new HashMap<>();
        graphMap.put("D",dNeighborMap);
        dNeighborMap.put("E",3);
        dNeighborMap.put("F",2);

        // E到达所有邻居节点的
        Map<String,Integer> eNeighborMap = new HashMap<>();
        graphMap.put("E",eNeighborMap);
        eNeighborMap.put("G",1);

        // F到达所有邻居节点的
        Map<String,Integer> fNeighborMap = new HashMap<>();
        graphMap.put("F",fNeighborMap);
        fNeighborMap.put("G",3);

    }

    // 到达节点的开销
    static Map<String,Integer> costMap = new HashMap<>();
    static {
        costMap.put("A",0);
        costMap.put("D",Integer.MAX_VALUE);
        costMap.put("C",Integer.MAX_VALUE);
        costMap.put("B",Integer.MAX_VALUE);
        costMap.put("E",Integer.MAX_VALUE);
        costMap.put("F",Integer.MAX_VALUE);
        costMap.put("G",Integer.MAX_VALUE);
    }

    // 处理过的节点
    static Set<String> processed = new HashSet<>();
    static {
        processed.add("A");
        processed.add("G");
    }


    // 存储父节点
    static Map<String,String> parentMap = new HashMap<>();

    static String start = "A";

    public static void main(String[] args) {

//        dijkstra();
        // 走完所有节点
        while (!processed.containsAll(graphMap.keySet())){
            dijkstra();
        }

        System.out.println(costMap.get("G"));

        // 所走路径
        String curNode = "G";
        StringBuilder route = new StringBuilder(curNode);

        while (!"A".equals(curNode)){
            route.insert(0,parentMap.get(curNode)+"->");
            curNode = parentMap.get(curNode);
        }

        System.out.println(route.toString());


    }

    private static void dijkstra() {
        String nextLowerNode = findLowerNode(start);
        if("".equals(nextLowerNode)){
            return;
        }

        // 从起点到该节点的花费时间
        Integer cost = costMap.get(nextLowerNode);

        int newCost = 0;
        // 该节点的所有邻居
        Map<String, Integer> allNeighbors = graphMap.get(nextLowerNode);
        for (Map.Entry<String, Integer> entry : allNeighbors.entrySet()) {
            newCost = cost + entry.getValue();
            if (costMap.get(entry.getKey()) > newCost) { // 如果经当前节点前往邻居节点更近，则更新该邻居的开销，
                costMap.put(entry.getKey(), newCost);
                parentMap.put(entry.getKey(), nextLowerNode); // 将该邻居的父节点设置为该节点
            }
        }
        // 该节点已被处理过
        processed.add(nextLowerNode);
    }

    public static String findLowerNode(String startNode){

        // 先找起点的邻居节点
        Map<String, Integer> nextNodes = graphMap.get(startNode);
        if(processed.containsAll(nextNodes.keySet())){ // 起点的邻居节点全都处理完了
            for(Map.Entry<String,Integer> entry : nextNodes.entrySet()){
                return findLowerNode(entry.getKey());

            }

        }else {
            int cost = Integer.MAX_VALUE;

            String nextNode = "";

            for(Map.Entry<String,Integer> entry : nextNodes.entrySet()){
                if(processed.contains(entry.getKey())){
                    continue;
                }
                // 距离该节点的花费
                if(entry.getValue() < cost){
                    cost = entry.getValue();
                    nextNode = entry.getKey();

                }
            }
            // 起点到该点的花费
            int newCost = costMap.get(startNode)+cost;
            if(newCost < costMap.get(nextNode)){
                costMap.put(nextNode,newCost);
                parentMap.put(nextNode,startNode);
            }
            return nextNode;
        }

        return "";
    }
}
相关文章

欢迎关注我的其它发布渠道

表情 | 预览
快来做第一个评论的人吧~
Powered By Valine
v1.3.10